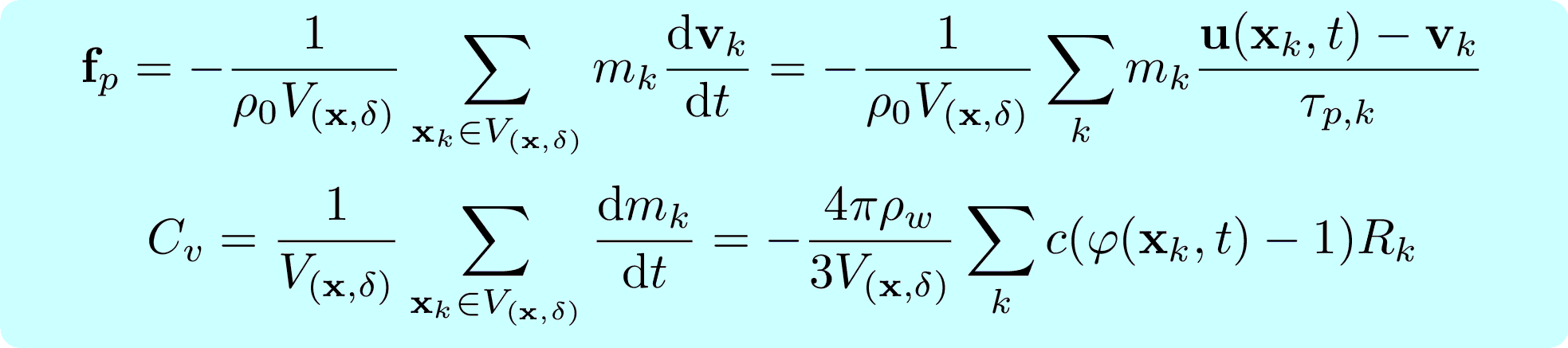Physical Model
- Details
- Last Updated on Wednesday, 14 December 2016 14:06
Droplet module (v1.4p only)
Version 1.4p contains a module for the Lagrangian tracking of droplets or inertial particles. The module tracks the motion of single droplets by solving the relevant momentum equations (Stokes drag & gravity):

Here, xk is the droplet position and vk is its velocity, while u is the fluid velocity in corrispondance of the droplet.
Moreover:
- Droplets are assumed to be spherical. The radius Rk of each droplet is considered to vary as function of the local relative humidity φ in correspondance of the droplet position.
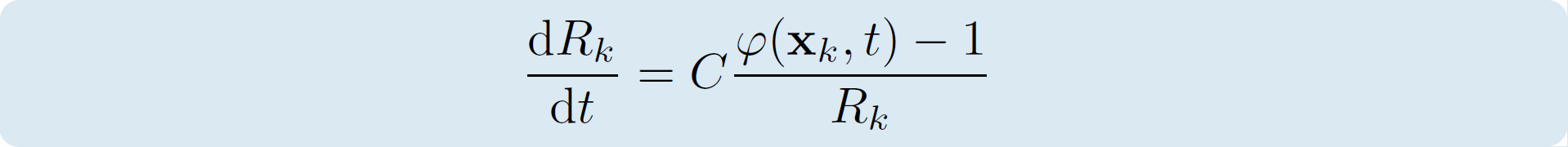 The coefficient C is given by
The coefficient C is given by 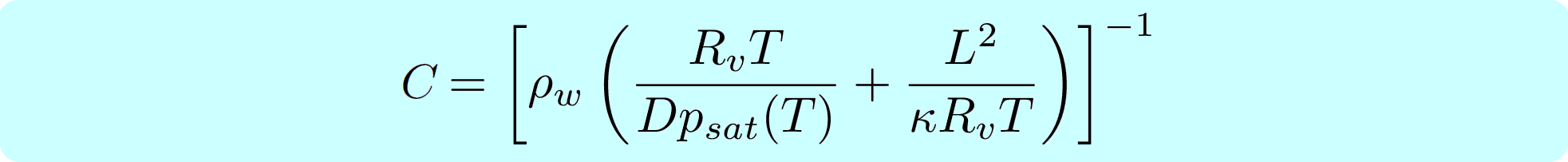 where L is the latent heat of evaporation/condensation, κ is the thermal diffusivity of air (Pr about 0.7), D is the diffusivity of vapour in air (Sc about 0.5), ρw is the water density and psat is the saturation pressure, approximated by the Clapeyron-Clausius law:
where L is the latent heat of evaporation/condensation, κ is the thermal diffusivity of air (Pr about 0.7), D is the diffusivity of vapour in air (Sc about 0.5), ρw is the water density and psat is the saturation pressure, approximated by the Clapeyron-Clausius law: 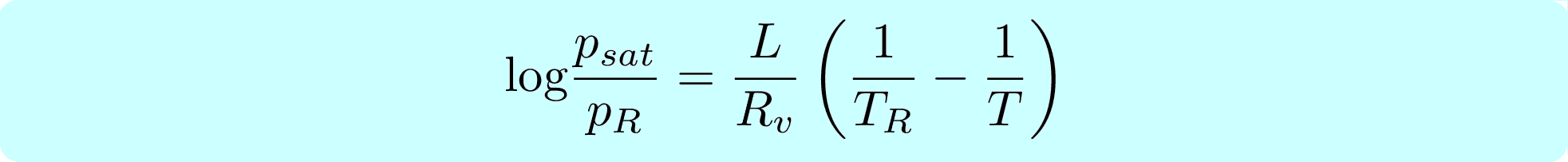 where pR is the saturation pressure at the reference temperature TR
where pR is the saturation pressure at the reference temperature TR - Droplets can collide. At each step, the module checks the occurrence of collisions among the droplets. The collision detection method is schematically described here, and carried out at each step.
- A momentum and (water) mass feedback of the droplets on the flow is considered (see below).
The module has been tested in version 1.4 (slab parallelization) and will be adapted to version 1.7 of the code (pencil parallelization).
Navier-Stokes (Boussinesq) equations
The code solves the Navier-Stokes equations together with up to 6 additional scalar equations. In versions 1.4strat and 1.4p the first two scalars represent temperature and water vapour density:
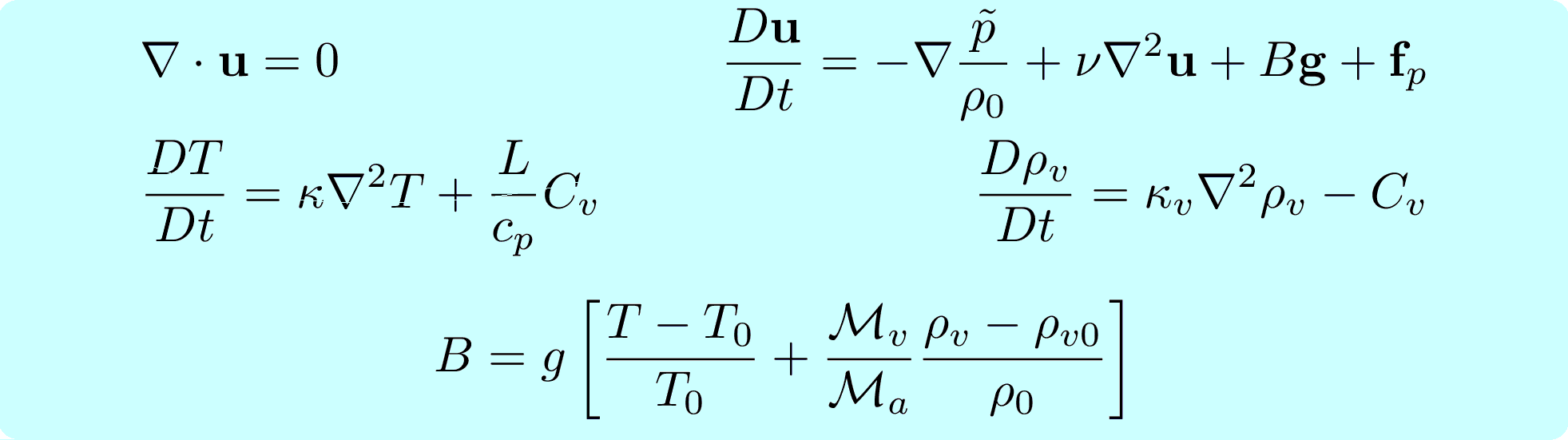
here L is the latent heat of evaporation/condensation, Cv is the condensation rate per unit volume, and fp is the particle force per unit volume on the fluid phase. The last two terms represent the momentum and mass feedback of the droplets to the fluid phase, and are linked to the equations for the droplets: