The GEOSCORE group

The GEOSCORE Group is located at the Dipertimento di Scienze Matematiche “Giuseppe Luigi Lagrange” of Politecnico di Torino, in Turin, Italy. The research activity of the group covers the numerical resolution of partial differential equations in fractured porous media, with particular focus to geoscience applications. Numerical simulations in fractured media are still a challenging task, requiring high computational resources. This is a consequence of the geometrical complexity of the domain, characterized by a large number of fractures forming intricate intersections, which are interfaces for the numerical solution.
The Group is active in the definition of unconventional discretization strategies to obtain a numerical solution to flow problems in underground media effectively and efficiently. Two main stragegies have been devised and are currently developed:

The DFM model

Fractures in a porous medium are regions characterized by a dramatic change of material properties, with one spatial dimension, the thickness, which is orders of magnitude smaller than the other two dimensions and than the whole domain. Fractures might have a significant impact on relevant flow characteristics, such as flow directionality, and for this reason, in many circumstances, their explicit representation is to be preferred to the use of upscaling techniques defining homogenized material properties. According to Discrete Fracture and Matrix (DFM) models, fractures in a porous material can be represented as planar interfaces of co-dimension one, thus overcoming the difficulty related to the simultaneous representation of the scale of fracture thickness and of domain size. Nevertheless, fractures can form an intricate network of intersections, thus generating extremely challenging computational domains.

Mesh generation issues

The generation of a mesh of such intricate networks is a non-trivial task if mesh elements are required to be conforming with fractures and intersections between fractures. Standard discretization techniques need meshes conforming to the interfaces in order to enforce suitable coupling conditions. The GEOSCORE Group has devised new strategies to overcome such complexity.

(left) Example of a fracture network in a porous material represented according to the DFM model. Porous matrix impervious. (right) Computed distribution of hydraulic head in the network with a non-conventional approach based on the numerical optimization on non-conforming meshes

Non conforming meshes

A first approach relies on meshes non conforming to the interfaces and relies on the numerical optimization to enforce the required coupling conditions. Mesh generation is then reduced to a trivial task. A cost functional is introduced expressing the error in the fulfillment of coupling conditions and the solution is seen as the minimum of this cost functional constrained by constitutive laws on the fractures and in the bulk material.

  • S. Berrone, S. Pieraccini, S. Scialò, Flow simulations in porous media with immersed intersecting fractures, Journal of Computational Physics 345 (2017) 768–791
  • S. Berrone, C. Fidelibus, S. Pieraccini, S. Scialò, F. Vicini, Unsteady advection-diffusion simulations in complex Discrete Fracture Networks with an optimization approach, Journal of Hydrology 566 (2018) 332–345
A Detail of a mesh non-conforming to fracture intersections (bottom-left) and a snapshot of the solution of an unsteady dispersion problem for a passive scalar in a network of fracture (impervious matrix).

Polyhedral conforming mesh

An alternative approach devised by the group relies on polyhedral conforming meshes. In this case, starting from a triangular/tetrahedral non-conforming mesh, a mesh conforming to the interfaces can be easily built simply cutting the original mesh according to the interfaces. New discretization methods, such as the Virtual Element Method, are then used on such polygonal/polyhedral meshes.

  • M. F. Benedetto, S. Berrone, A. Borio, S. Pieraccini, S. Scialò, A hybrid mortar virtual element method for discrete fracture network simulations, Journal of Computational Physics 306 (2016) 148–166
  • S. Berrone, A. Borio, C. Fidelibus, S. Pieraccini, S. Scialò, F. Vicini, Advanced computation of steady-state fluid flow in Discrete Fracture-Matrix models: FEM–BEM and VEM–VEM fracture-block coupling, GEM - International Journal on Geomathematics (2018) 9:377–399
Computed solution in a block of porous material with fractures using polygonal/polyhedral meshes and the VEM

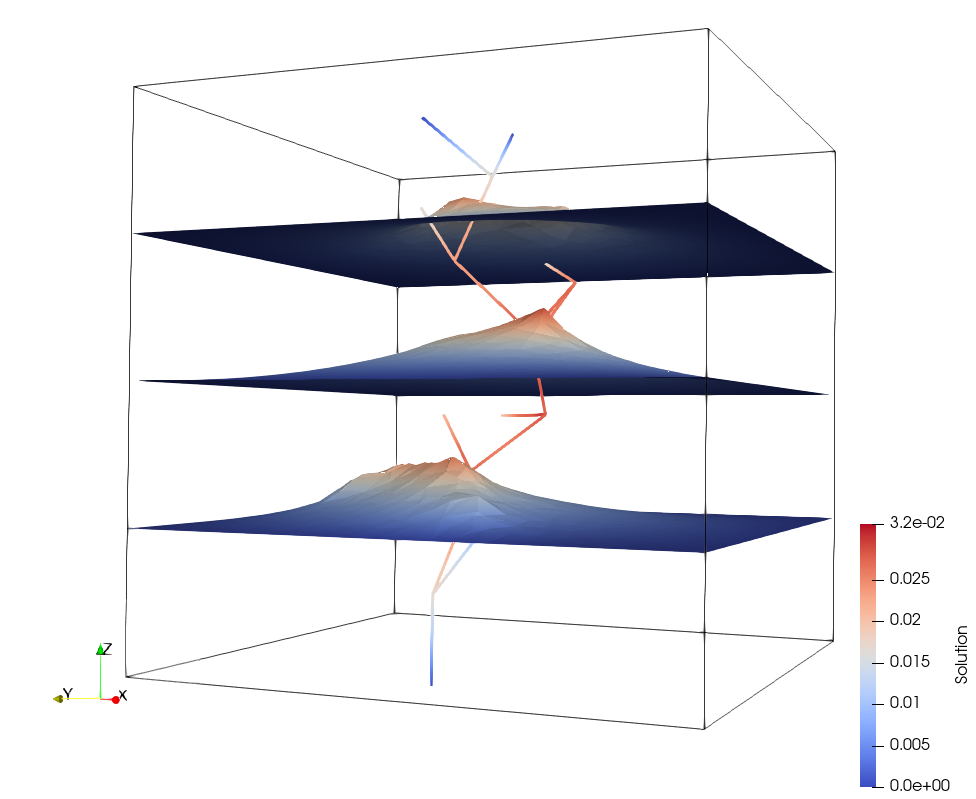
3D-1D coupled problems

Coupled 3D-1D problems arise from the geometrical reduction of domain configurations presenting small tubular inclusions embedded in a larger domain. When the diameter of the inclusion is much smaller than its lenght and than domain size, from a simulation standpoint, it is convenient to represent each inclusion as a 1D domain, thus neglecting solution variations along the radius. The mathematical description of coupled problems on geometrical domains with a dimensionality gap higher than one is not striaghtforward, as no bounded trace operator is defined in standard functional spaces on manifolds with a high dimensionality gap, such that ad hoc formulations and numerical schemes are needed. The problems in the bulk 3D domain and in the small inclusions are splitted resorting to a three-field based domain decomposition method and the coupling is restored through the minimization of a functional.

  • S. Berrone, D. Grappein, S. Scialò, 3D-1D coupling on non conforming meshes via a three-field optimization based domain decomposition, Journal of Computational Physics 448 (2022)
Computed solution in a block of material with a ramified inclusion