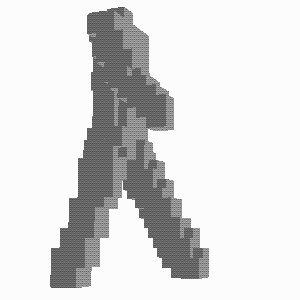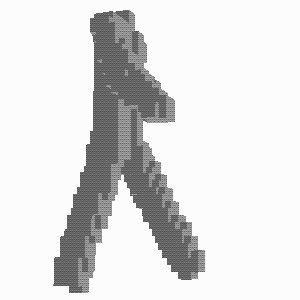back to Projects page
Introduction
Capturing the motion of the human body is an important practical issue.
Realistic animation of 3-D characters for movies, TV and 3-D games are
driven by motion data obtained from human performers. Many other application areas
exist, as telerobotics, ergonomics, crash simulation with dummies, biomechanics and
sport performance analysis. Several commercial "motion capture" (MC) equipment exist
at present. They are based on the idea
of tracking key points, usually joints, of the subject. This can be done with either of
two technologies: magnetic and optical tracking. Magnetic tracking requires one or
more transmitters to produce a magnetic field in a working volume. Sensors located
at key points on the body supply up to six position an orientation data.
Optical tracking requires optical markers, active or reflective.
Their light is captured by TV cameras and a computer works out their 3-D positions.
Usually markers are less bulky than magnetic sensors, but can be occluded by the body
of the performer.
Both techniques require more or less bulky objects to be attached to the body.
These objects disturb the subject and more or less affect his gestures.
For some application, as analyzing sport performances, this could be a serious drawback.
Also observe that both techniques supplies data for a rather limited number of points.
The purpose of our work is to develop an alternative approach, on one hand capable
of overcoming the problems highlighted for commercial devices in some application areas,
and on the other hand sufficiently simple and robust as to allow the implementation of practical
equipment. Our approach is based on multiple 2-D silhouettes of the body extracted from 2-D images.
Silhouettes are easy to obtain from intensity images. The approach is not intrusive:
no devices attached to the body is required. From silhouettes: i) a direct reconstruction of
the 3-D shape of the body can be computed with a technique known as volume intersection (VI),
and ii) the 3-D posture and motion of models of the human body can be obtained by fitting a model
to the reconstructed volume.
The number and position of the cameras, which are subject to practical constrains,
strongly affect the accuracy of the reconstruction of the human body, and of the
estimation of posture and motion of a model. The purpose of this work
is twofold: 1) demonstrating in a virtual environment a system based on this approach; 2)
investigating the precision of both 3-D direct reconstruction, and model-based posture and
motion identification, for several postures of the body, different arrangements of cameras
and various resolutions.
The Virtual Environment and Motion Capture System
The Model
The skeleton of the human body has been modeled as a tree of 14 rigid segments connected
by ball joints (see Fig.1(a)). The lengths of the segments agree with the average measures
of the male population. The body is modeled by cylinders of various width centered about
the segments (see Fig.1(b)), except for the trunk, whose section is a rectangle with smoothed angles.
Specifying a posture requires to specify a vector containing 31 parameters (three coordinates for
the radix of the tree and two angles for each segment). The dummy can assume different postures. A
convenient program can drive the dummy in a walk that is sufficiently realistic for our purposes.
In Fig. 2 we show some images of the walking dummy.
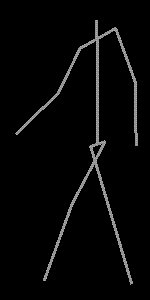
Fig. 1 (a) and (b)
Cameras and Silhouettes
Any number of stationary cameras can be located anywhere in the virtual 3-D environment
(see for instance Fig. 3). Each camera is defined according to the Tsai’s camera model.
Its position and orientation are specified with a view center, an optical axis, and an up vector.
The camera provides in the image plane a frame of 512·512 pixels. Each pixel has two levels for representing
the silhouette and the rest of the image. The silhouettes have been obtained using Open GL.
Fig. 2 Images of the walking dummy
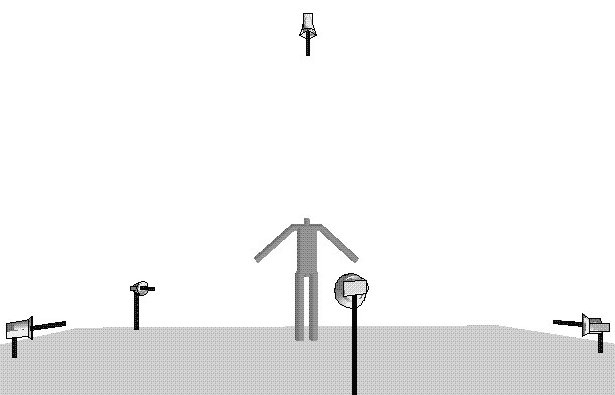
Fig. 3 The virtual environment with 5 cameras
The Volume Intersection Algorithm
The back-projection of the silhouettes can be performed
using Tsai’s camera model and calibration data, consisting in a set of 3-D world coordinates of
feature points and the corresponding 2-D coordinates (in pixels) of the feature points in the image.
The VI algorithm outputs the voxels containing the boundary of the reconstructed volume R.
This makes the time of the algorithm dependent on the number of surface voxel, and thus approximately
on the square of the linear resolution. The reconstruction can be performed with various resolutions.
In Fig. 4 we show some outputs of the
VI algorithm at various resolutions.
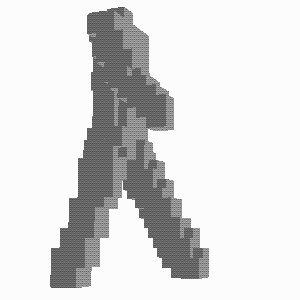
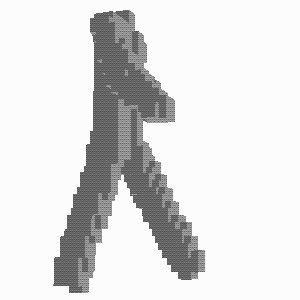
Fig. 4 - The original posture and the volumes reconstructed at increasing resolutions
(voxel sizes of 49, 35 and 21 mm)
Determining the Posture of the Model
Fitting the model to the volume R obtained by VI requires to minimize some measure of
distance between the dummy and the volume reconstructed. To this purpose, we consider
the squared distances between the centers of the boundary voxels and the skeleton of the dummy.
More precisely, we assign to each center the smallest of all the distances from the segments of the
skeleton.
Recovering the Motion of the Model
In order to recover the motion of the dummy, the above procedure is applied several
times to sets of silhouettes obtained from multiple sequences of frames. Exception
made for the first time, the starting position of the model is that obtained from the previous
set of silhouettes. Since each time the dummy is very close to its final position, the computation
of the posture requires relatively few steps. In addition, some sort of implicit filtering takes
place, since possible local minima of the distance function due to "phantom" volumes are avoided.
The sequence of postures obtained are affected by two kinds of errors: discretization errors
and errors due to the VI approach. In a real environment, further errors are due to the uncertain
boundaries of the silhouettes.
Demo
Not a real demo yet. Some .mov files showing how the system works.
vi.mov (1181 kb) showing how VI algorithm works
(blue points are voxel centers)
reconstruction.mov (3066 kb) showing reconstruction process
(blue points are voxel centers, green is the reference model, brown the reconstructed one)
