Hydrodynamic Stability

Details

Last Updated on Monday, 19 January 2015 10:13

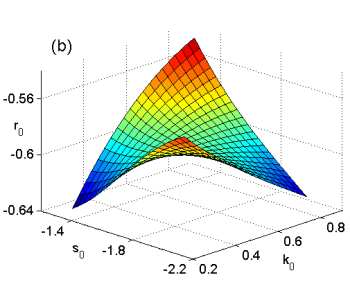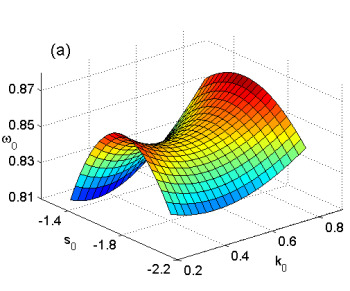
Figure 1. Bluff-body wake. Saddle points multidimensional map: (a) ω₀(k₀,s₀) and (b) r₀(k₀,s₀), Re=35, 4 diameters downstream the body.

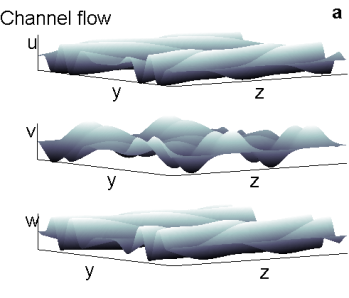
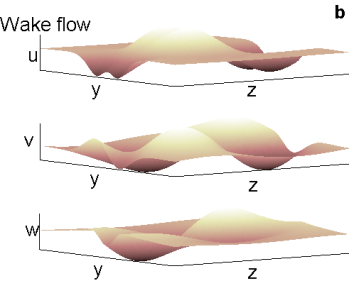
Figure 2. Snapshots of the perturbation velocity field in the physical plane (y, z) normal to the streamwise direction, x. (a) Channel flow: Re = 10000, t = 20, ϕ = 3/8 π, antisymmetric initial condition, k = 1.5. (b) Wake flow: Re = 100, wake section: 50 body lengths downstream, t = 45, ϕ = 3/8 π, antisymmetric initial condition, k = 0.7.

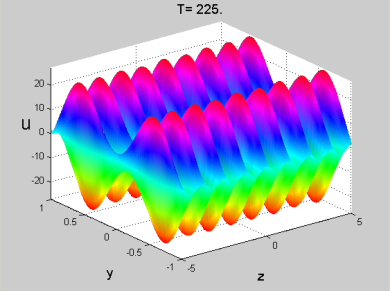Figure 3. Longitudinal component of the perturbation velocity field in the physical plane (y, z) normal to the streamwise direction, x.  Poiseuille channel flow: Re = 10000, t = 225, ϕ =  π/2, antisymmetric initial condition, k = 5. See the MOVIE for the complete temporal evolution.

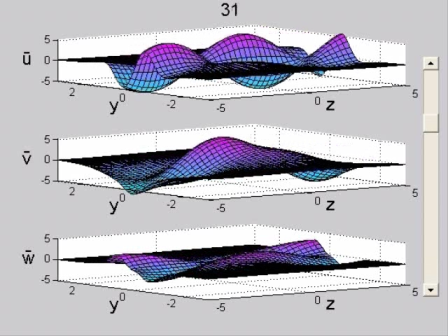		Figure 4. Amplified configuration. Wake flow (R=100, x_0=10, k=1.7, symmetric initial condition, Φ=π/8).  Perturbation velocity field in the physical plane (y, z) normal to the streamwise direction, x.   See the MOVIE for the complete temporal evolution.
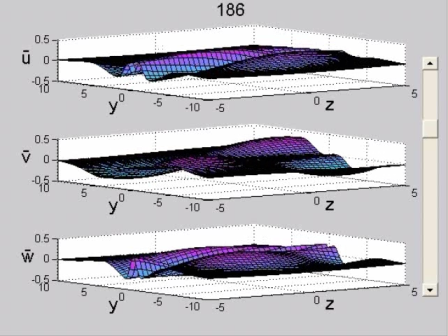		Figure 5. Weakly amplified configuration. Wake flow (R=100, x_0=10, k=0.6, asymmetric initial condition, Φ=π/4).  Perturbation velocity field in the physical plane (y, z) normal to the streamwise direction, x.   See the MOVIE for the complete temporal evolution.
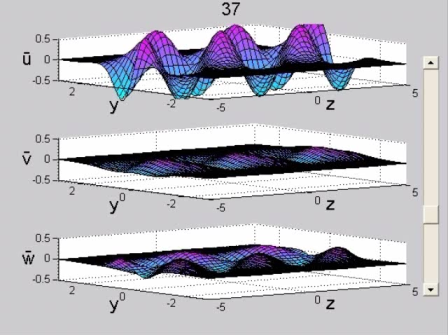		Figure 6. Damped configuration. Wake flow (R=100, x_0=10, k=1.7, symmetric initial condition, Φ=3/8π). Perturbation velocity field in the physical plane (y, z) normal to the streamwise direction, x.   See the MOVIE for the complete temporal evolution.