Large-Eddy Simulation of Turbulent Flows

Details

Last Updated on Tuesday, 26 June 2012 23:46

•  Angular momentum model. The equation for the intrinsic moment of momentum averaged over small volumes of linear dimension δ have been considered and a representation of it is given as an infinite sequence of independent equations using a series expansion in terms of δ^2. The equations of different orders are obtained through linear antisymmetric operators — with a structure that is similar to that of the curl — acting on the momentum equation. The first-order term of the sequence is the Helmholtz equation; the remaining terms can be considered as balances for a kind of higher-orders vorticity. It has been shown that the coupling between the momentum and the angular momentum equation, based on a supposed antisymmetrical part of the stress tensor — which, in the past, has sometimes been assumed by authors who deal with turbulent flow of a homogeneous fluid — is devoid of physical rationale. A different form of coupling is proposed that may be used to describe a turbulent flow of a homogeneous medium, using a large eddy simulation technique. In the authors model the coupling is given by a functional dependence of the turbulent eddy diffusivity over the angular momentum of a finite volume of a fluid. (See Phys.Fluids 14 (2002))

• Non commutation terms in the LES. A simple procedure to approximate the noncommutation terms that arise whenever it is necessary to use a variable scale filtering of the motion equations and to compensate directly the flow solutions from the commutation error has been proposed for the first time. Such a situation usually concerns large eddy simulation of nonhomogeneous turbulent flows. The noncommutation of the average and differentiation operations leads to nonhomogeneous terms in the motion equations, that act as source terms of intensity which depend on the gradient of the filter scale d and which, if neglected, induce a systematic error throughout the solution. We determined the different noncommutation terms of the motion equation as functions of the δ gradient and of the δ derivatives of the filtered variables. We have shown that approximated noncommutation terms of the fourth order of accuracy, with respect to the filtering scale, can be obtained using series expansions in the filter width of approximations based on finite differences and introducing successive levels of filtering, which makes it suitable to use in conjunction with dynamic or mixed subgrid models. The procedure operates in a way which is independent of the type of filter in use and without increasing the differential order of the equations, which, on the contrary, would require additional boundary conditions. (See Phys.Fluids 15 (2003))

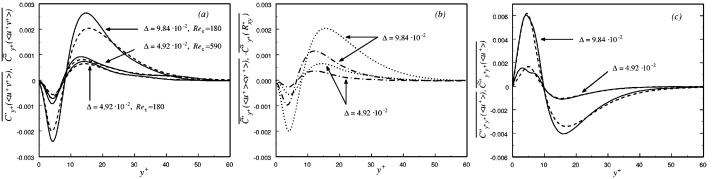
Figure 1. A priori test of the non-commutation terms approximation in a channel flow at Re_τ =180. (a) Continuous line: Average values of the exact noncommutation convection term. Dashed line: correspondent average values predicted by the procedure. (b) Noncommutation approximated terms for the resolved Reynolds stresses (dash-dotted line) and for the subgrid scale stresses (dashed line). (c) Average values of the noncommutation diffusive term (continuous line) and the correspondent values predicted by the procedure (dashed line).

• Approximate boundary conditions. Two different types of instantaneous wall boundary conditions have been proposed for resolved large scale simulations that extend inside the viscous sublayer. These conditions transfer the physical no-slip and impermeability/permeability information, which can only be rigorously applied to the unfiltered variables, to the filtered variables. The first condition is universal, while the second one specifies the wall stress and relevant distribution and can be used to treat inverse flow problems. The filter scale close to the wall is a function which varies according to its position and thus the problem of the noncommutation of the filter and differentiation operators arises. Used together with the explicit noncommutation procedure by Iovieno and Tordella, these boundary conditions constitute a wall treatment which could improve the use of the large-eddy methodology in relation to aspects that are independent of the modeling of the subgrid scale motion. When applied in the test case of the plane periodic channel, intentionally using the most crude subgrid scale model (Smagorinsky, with no dynamic procedure or wall damping function) to prove its efficacy, the proposed near-wall treatment yielded resolved large-eddy simulations which compare well with both direct numerical simulations and with experimental data. (See Phys.Fluids 16 (2004) and ETC-10)

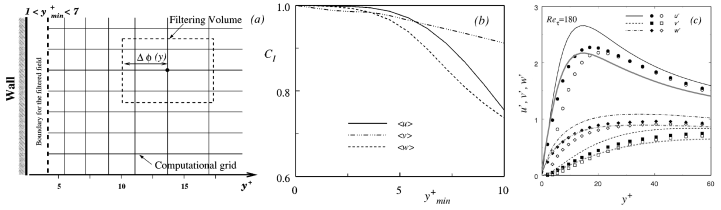
Figure 2.  (a) A schematic view of the shifted boundary conditions, the filter, and the grid. (b) An a priori test on the approximate boundary conditions: correlation level as a function of the distance y_min of the shifted boundary from the wall at Re_τ =180, boundary condition I. (c) Resolvable turbulence intensities, comparison between LES (filled symbols: boundary condition I, open symbols: boundary condition II) and direct simulations (thin lines: DNS, thick lines: filtered DNS).

• Selective Large-Eddy simulation. Application to hypersonic jets. A method for the localization of small scales in turbulent velocity fields is proposed. This method is based on the introduction of a scalar probe function f which represents the magnitude of the twisting-stretching term normalized with the enstrophy. The statistical analysis of a homogeneous and isotropic high Reynolds number (Re__λ = 280) turbulence field shows that, for a fully developed turbulent field of fluctuations, the probability that f is larger than 2 is almost zero, while, for an unresolved field, is finite. By computing f in each instantaneous realization of the simulation it is possible to locate the regions where the magnitude of the normalized stretching-twisting is anomalously high. This allows the identification of the regions where the subgrid model should be introduced into the governing equations (selective filtering). The localization criterion is independent of the subgrid scale model used in a possible Large-Eddy Simulation carried out after the small scale localization is obtained. This method for the localization of the regions where the turbulent fluctuations are unresolved is applied to the selective large-eddy simulation (LES) of a time volving compressible turbulent jet with an initial Mach number equal to 5. (see CPC (2008) and DLES-7).

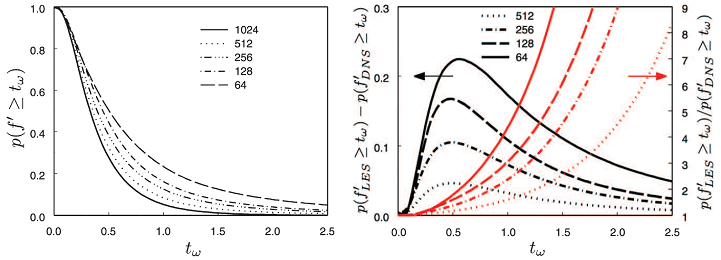
Figure 3. (a) Distribution of the probability of having f larger than a given threshold t_{_ω} for different resolutions of incompressible homogeneous and isotropic turbulence (sensor f__DNS for resolution 1024^{^3}, sensor f_{_LES} for the filtered fields); (b) (left ordinate, black curves) difference between the probability in the filtered fields and in the unfiltered field, (right ordinate, red curves) ratio between the probability in the filtered fields and in the unfiltered field.

Some visualizations of the selective large-eddy simulation of the jet can be seen in the gallery.