Solar-wind turbulence

Details

Last Updated on Thursday, 09 March 2017 15:50

The NASA Voyager Interstellar Mission explores the outer heliosphere and its interaction with the local interstellar medium (LISM). Beyond any expectation, the Voyager 1 and 2 (V1, V2) spacecrafts will send data until 2025 and they are providing the first and unique in situ measurements at the edge of the heliosphere. Plasma and magnetic field fluctuations are ubiquitous in the solar-wind. Waves, weak and strong turbulence, waves, shocks, coherent structures, etc. coexist in the system, and discriminating the different phenomenologies is still a challenging target.

In order to characterize the multi-scale nature of solar-wind fluctuations and identify the scales for which a power-law for the energy decay applies, a spectral analysis over a wide frequency range is desirable. It should be noted that to achieve this goal the uncertainty in the spectral slope has to be kept below 10%. Moreover, analysis in the outer heliosphere are needed to understand the evolution of such fluctuations in space and time. Unfortunately, data gaps represent a severe limitation to spectral analysis of solar-wind data, especially at heliocentric distances larger that 1 Astronomical Unit (AU). In fact, data from the Voyagers contain gaps that typically become larger and irregularly distributed as the crafts move away from the sun (30% of data are missing at 5 AU, 70-97% in the heliosheath).

From the data  recorded by the Voyager 2 mission, we can resolve the velocity and particle density fluctuations between 10^-8 and 4x10^-3 Hz, i.e. in the MHD energy-injection and inertial ranges of solar wind. Till now, we considered datasets from: 1979 data, acquired when Voyager 2 was at about 5 astronomical units from the sun, and 2007-2013 data from V1 and V2 in the heliosheath.

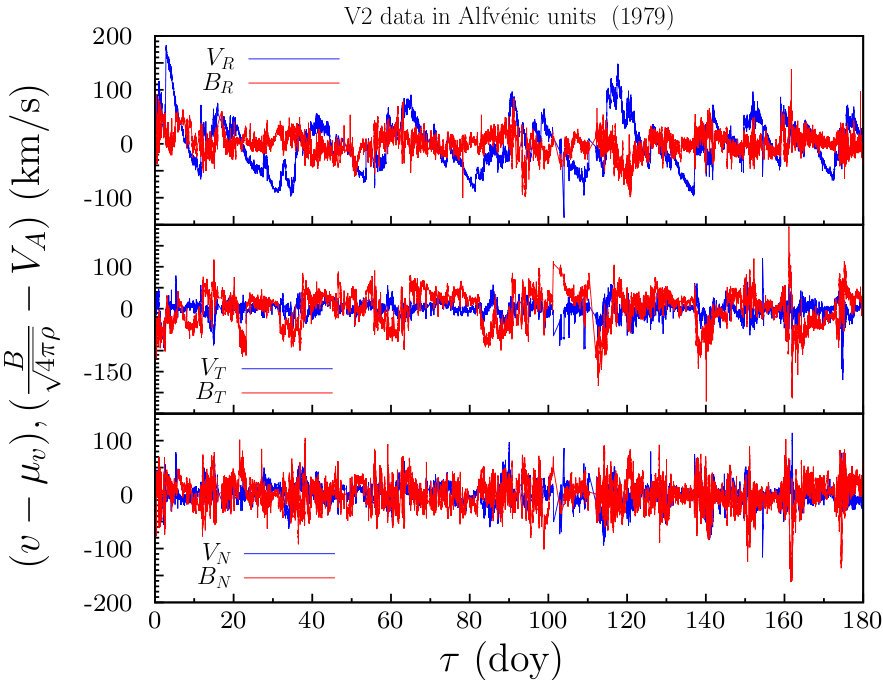
Figure 1. Velocity and magnetic field data from V2, year 1979 (DOY 1-180). Components in RTN heliographic reference frame.

Spectral recovery methodology.  Historically the Blackman-Tukey method has been widely used. However, for large amounts of missing data (> 30%), this computation suffer from a bad convergence to the true correlation function, leading to wrong spectral slopes and unphysical energy peaks in the power spectrum. The following techniques were proposed by us: (i) Windowed averaged Fourier transforms of contiguous subsets; (ii) Fourier transform of the correlation function coupled to linear interpolation; (iii) Maximum likelihood stochastic reconstruction; (iv) Compressed sensing spectral estimation - to our knowledge, it was the first time that such technique was applied to the turbulence/astrophysical context. (v) Model-spectra from genetic optimization procedure. Details can be found in two papers published by our group [1, 2]. The quality of each technique was verified on reference synthetic data sets having known spectral properties. Solar-wind contiguous data (Ulysses measurements in 1990-1991) were also considered as an alternative test base. The same distribution of gaps as in Voyagers’ data were projected on the reference signal, in order to estimate the spectral error for each methodology. The error in the spectral slope was between 3% and 10% for all the cases analyzed.

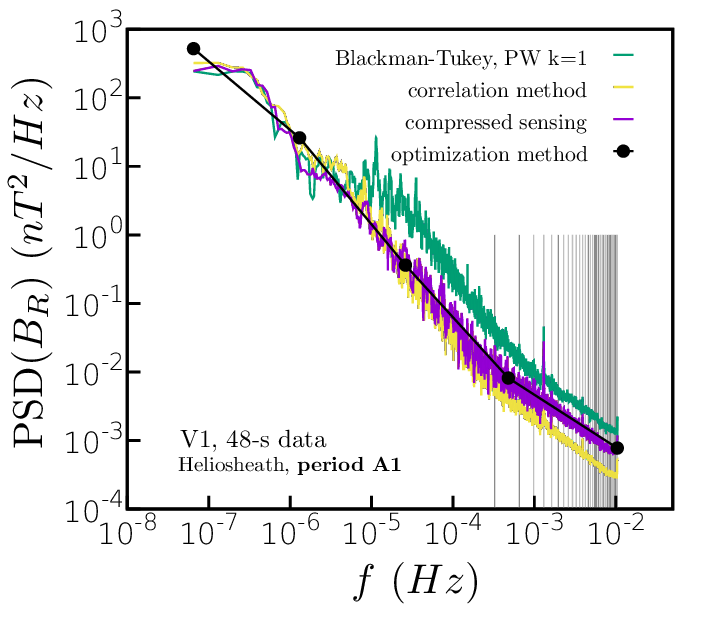Figure 2. Left: convergence of the correlation function, C, for a synthetic data-set. Comparison between linear interpolation and the Blackman-Tukey method. Right: spectra computation from heliosheath V2 data, comparison of different techniques.

Results: solar-wind at 5 AU. The 1979 spectra of all variables show a power law scaling with exponents in between -1.5 and -1.8. PDFs and correlations indicate that the flow has a significant intermittency. The reliability of the reconstruction methods used is analyzed by introducing the same sequence of gaps observed in the Voyager data into a reference dataset extracted from direct numerical simulations of incompressible Navier-Stokes turbulence as well as from synthetic turbulence, and then by comparing the statistics obtained with those of the complete reference dataset.