You are here: Home Research Hydrodynamic Stability of Shear Flows

Hydrodynamic Stability of Shear Flows

Details
Last Updated on Sunday, 22 April 2012 15:45

The hydrodynamic stability of fluid flows is an important subject in different fields, such as aerodynamics, mechanics, astrophysics, oceanography, atmospheric sciences, and biology. Stability can be defined as the ability of a dynamical system to be immune to small disturbances. In general, a system excited with infinitesimal perturbations is considered stable if the initial state of equilibrium, in the short or long term, is reached again. On the contrary, a system is unstable if, subject to small oscillations, it departs from any state of equilibrium.
The central issue of the stability analysis is to understand the underlying reasons for the breakdown of laminar flow and its subsequent transition to turbulence. Although many improvements have been made over a hundred years, this remains an open question and a definitive means for prediction is still to be found.


Linear modal analysis

We focus on the long-term evolution of disturbances described through modal analysis, a method which allows the determination of the asymptotic stability of a flow. The stability of the intermediate and far near-parallel wake is studied by means of a multiscale approach. The disturbance is defined as the local wavenumber at order zero in the longitudinal direction and is associated to a classical spatio-temporal WKBJ analysis. The inverse of the Reynolds number is taken as the small parameter for the multiscaling. It takes into account non-parallelism effects related to the transversal dynamics of the base flow. The first order corrections find absolute instability pockets in the first part of the intermediate wake (and not in the near wake, where the recirculating eddies are, as usually seen in literature in contrast with the near-parallelism hypothesis), see Fig. 1. These regions are present for Reynolds numbers larger than Re = 35. That is in agreement with the general notion of critical Reynolds number for the onset of the first instability of about Re = 47.

Figure 1. Instability characteristics at order 0 (thin curves) and at order 0+1 (thick curves): (a) wavenumber, (b) spatial growth rate, (c) pulsation, and (d) temporal growth rate; R=35, 50, and 100.

 

In particular, for Re = 50 and Re = 100, the angular frequency obtained is in agreement with global data in literature concerning numerical and experimental results (see Fig. 2). The instability is convective throughout the domain. All the stability characteristics are vanishing in the far field, a fact that is independently confirmed by the asymptotic analysis of the Orr-Sommerfeld operator. 

 
















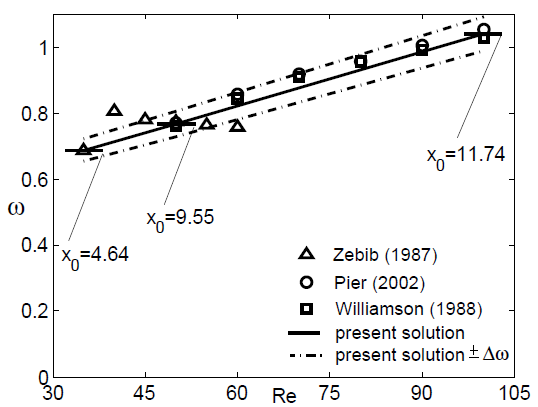
Figure 2. Comparison between the global pulsation data according to Pier (2002), Zebib (1987), Williamson (1988), and present modal solution (accuracy Δω=0.05).


Linear nonmodal analysis: initial-value problem formulation

The stability analysis of different shear flows (Poiseuille and Couette channel, two-dimensional wake, two- and three-dimensional boundary layer flows) is studied as an initial-value problem to observe the transient behaviour and the asymptotic state of perturbations initially imposed. The transient dynamics offers a great variety of different behaviours and phenomena, which are not a priori easy to predict (see some examples in Fig. 3). 

 

 

 

Figure 3. Collection of transient lives (left: channel, right: wake) of the perturbations observed through the amplification factor, G (top), and the frequency, ω (bottom). Top: energy transients variation with changes in the wavenumber magnitude. Bottom: the temporal evolution of the frequency highlights the typical formation of time scales others than the flow external time scale and the wave period.

 

Before the asymptotic state is reached, high maxima of energy followed by asymptotic damping or very low minima of energy reached before the ultimate amplification occurs are just some relevant examples of the observed scenarios for transients lasting thousands of time scales. Though the dynamics we consider is linear, different temporal scales develop for each wavelength. For instance, the system exhibits two distinct periodicity, one of transient nature and the other of asymptotic nature. The transition from the early dynamics to the asymptotic state does not smoothly occur: frequency discontinuities appear as the ultimate state is approached (see Fig. 4).

 

 

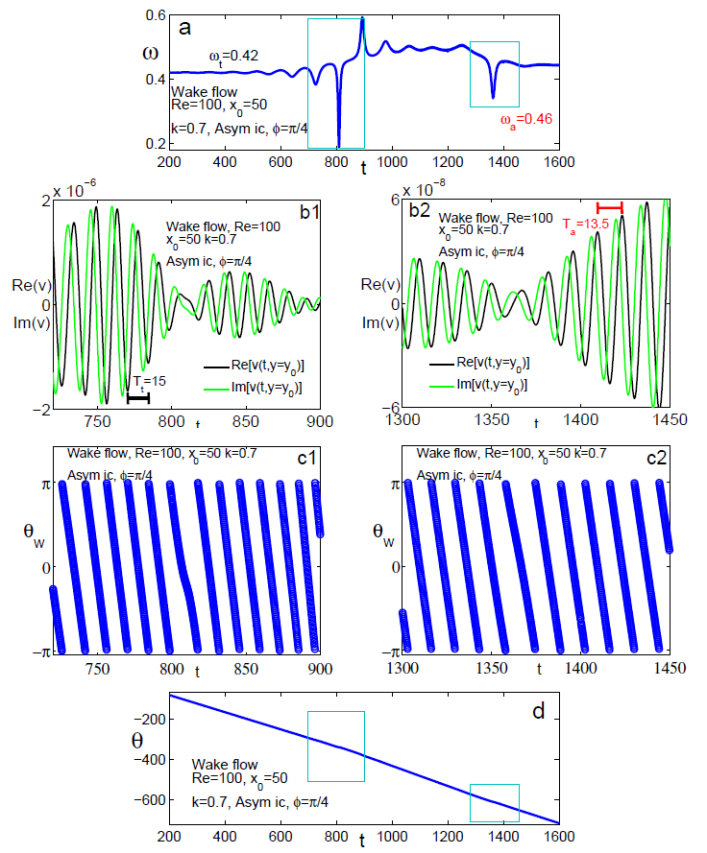
Figure 4. Wake flow, Re = 100, x_0 = 50, k = 0.7, symmetric input, ϕ = π/4, y0 = 1. (a) Temporal frequency evolution: transient (ω_t) and asymptotic (ω_a) frequency. (b1)-(b2) Perturbation transversal velocity v (real and imaginary parts) near the frequency jumps highlighted in part (a) with blue rectangles (Tt: transient period, Ta: asymptotic period). (c) Wrapped wave phase, θ_w(t) near the frequency jumps highlighted in part (a) with blue rectangles. (d) Unwrapped wave phase, θ(t). Blue rectangles highlight the temporal ranges where the frequency jumps occur.

 

In the temporal asymptotics, the initial-value problem well reproduces modal results in terms of angular frequency and temporal growth rate. Moreover, for the two-dimensional wake when the Reynolds number is larger than the critical one (Re_cr = 47), the present method gives a good prediction, in terms of wavelength and pulsation, of the vortex shedding observed in experiments (see Fig. 5).

 

 

 

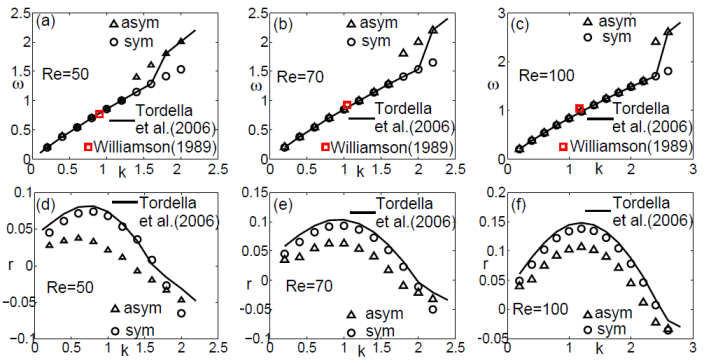
Figure 5. Wake flow (α_i = 0.05, Φ = 0, x_0 = 10, Re = 50; 70; 100). Asymptotic frequency ω (a, b, c) and temporal growth rate r (d, e, f) for initial-value problem results (black triangles and circles), modal analysis  (solid curves) and experimental data by Williamson (1989, red squares).

 

In the framework of the initial-value problem formulation, a multiscale analysis for the stability of long waves has been proposed. Even to the lowest order, the multiscaling - whose small parameter is defined as the polar wavenumber - approximates sufficiently well the full problem solution with a relevant reduction of the computational cost.

The two (modal and nonmodal) analyses combined together lead to a quite rich description of the shear flows stability.

A gallery of images and movies on instability and travelling waves can be found here.

 

Publications

Credits