RESEARCH
|
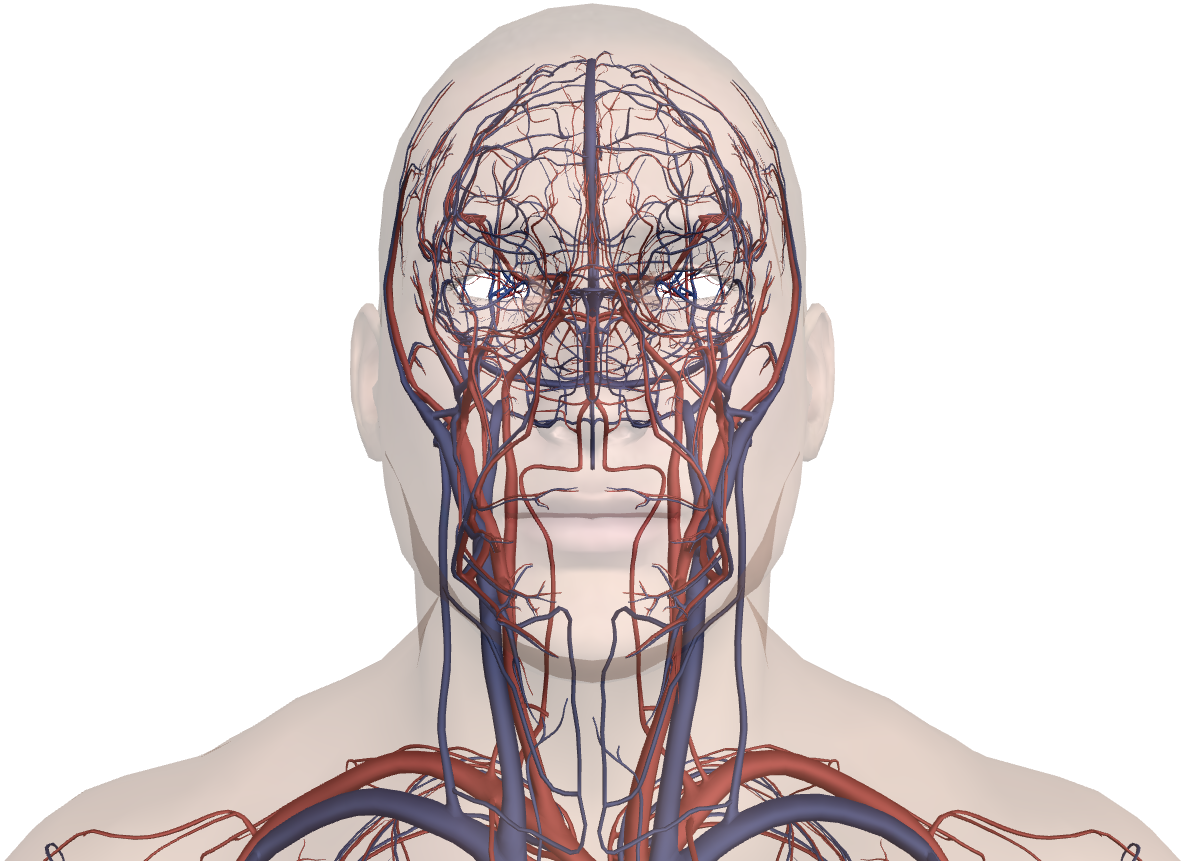
The cardiovascular dynamics is studied by means of lumped (0D) and multiscale (0D-1D) models. The lumped parameterization, consisting of a network of compliances, resistances, and inductances, allows to describe the complete cardiovascular system: the pumping heart together with the systemic and pulmonary circuits. The multiscale model focuses on the heart-arterial interaction. A lumped parameterization of the left heart and distal circulation is implemented, while 1D modeling of large-to-medium systemic arteries is accounted for. The modeling resolution leads to describe the cardiovascular system in terms of the characteristic fluid dynamics variables (pressures, volumes, flow rates) and the hemodynamic parameters able to evaluate the cardiac efficiency and performance. Read more... |
|
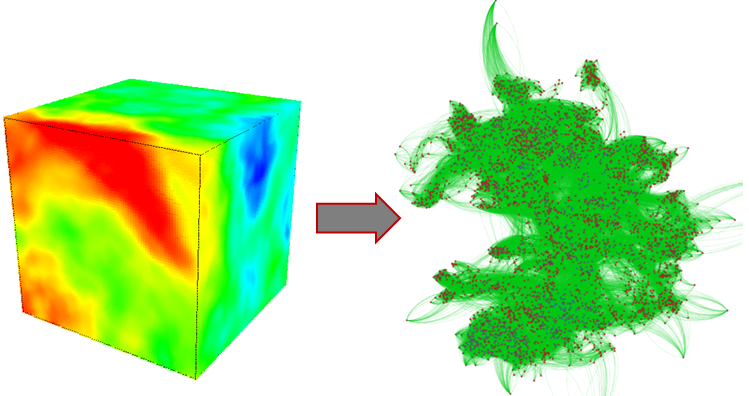
By combining graph theory and statistical physics, complex network theory provides a powerful tool to investigate the structure and function of complex systems with a large number of interacting elements. The development and characterization of complex networks makes their application suitable to analyze a wide range of systems from nature to economy, from engineering to society. Beside the well-established applications to Internet and World Wide Web, neural connections and social dynamics, complex networks have been successfully used to study many different phenomena such as, for example, human migration, cancer metastasis and earthquake occurrence. Read more...
|
|
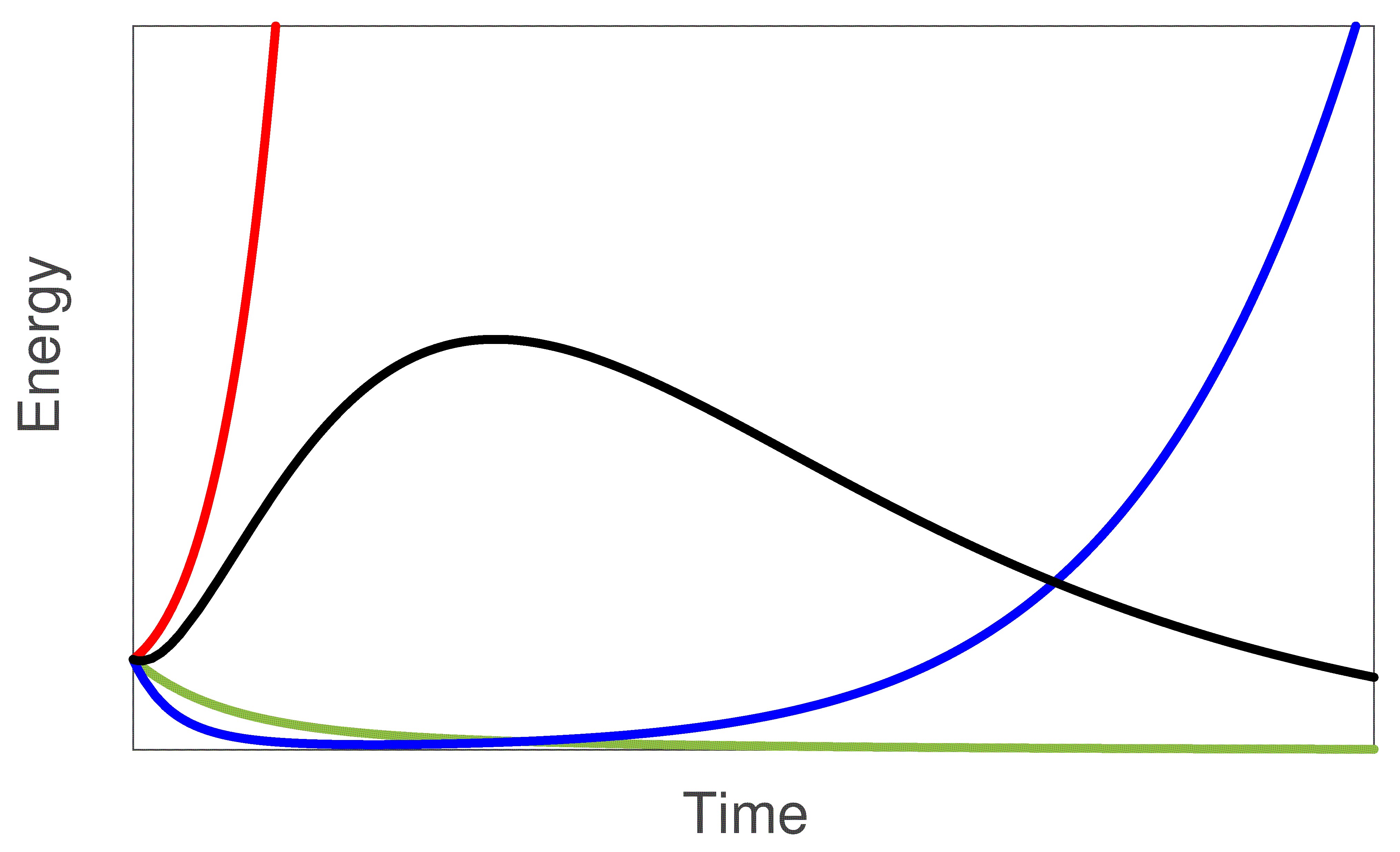
The hydrodynamic stability of fluid flows is an important subject in different fields, such as aerodynamics, mechanics, astrophysics, oceanography, atmospheric sciences, and biology. Stability can be defined as the ability of a dynamical system to be immune to small disturbances. In general, a system excited with infinitesimal perturbations is considered stable if the initial state of equilibrium, in the short or long term, is reached again. On the contrary, a system is unstable if, subject to small oscillations, it departs from any state of equilibrium. The central issue of the stability analysis is to understand the underlying reasons for the breakdown of laminar flow and its subsequent transition to turbulence. Read more...
|
|
Spatial patterns are widely present in different natural dynamical systems. Their occurrence has been studied for quite a long time with several applications in different fields, from hydrodynamic systems (e.g. Rayleigh-Bénard convection), plant ecosystems (e.g. dryland and riparian vegetation), to biochemical and neural systems. The study of patterns can offer useful information on the underlying processes causing possible changes of the system. Deterministic mechanisms in pattern formation have been widely studied, while stochastic models have only been developed more recently. They explain pattern formation as a noise-induced effect in the sense that patterns can emerge as a consequence of the randomness of the system's fluctuations. Read more...
|