

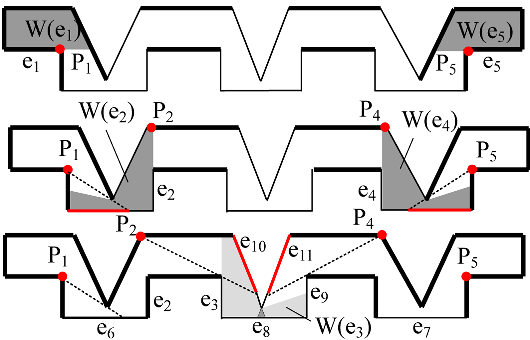
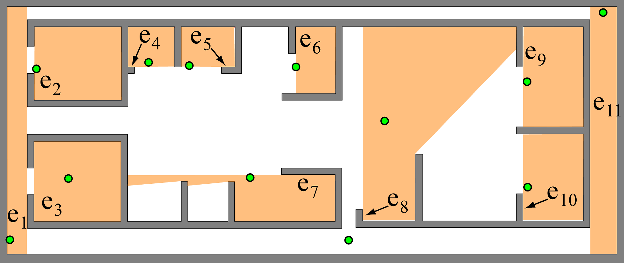
Locating visual sensors in 2D can be often modeled as an Art Gallery problem. Tasks such as surveillance require observing or “covering” the interior of a polygon with a minimum number of sensors or “guards”. For other tasks, such as inspection and image based rendering, observing the boundaries of the environment is sufficient. As Interior Covering (IC), also Edge Covering (EC) is NP-hard, and no finite algorithm is known for its exact solution. Approximate EC solutions are provided by many heuristic algorithms, but their performances with respect to optimality (minimum number of sensors) is unknown.
We have developed a new EC sensors location technique. The algorithm is incremental, and converges toward the optimal solution. It refines an initial approximation provided by an integer covering algorithm (IEC) where each edge is observed entirely by at least one sensor. A lower bound for the number of sensors, specific of the polygon considered, is used at each step for evaluating the quality of the current solution, and a set of rules are provided for performing a local refinement in order to reduce the computation. The algorithm has been implemented, and tests over hundreds of random polygons show that it supplies solutions very close to and often coincident with the lower bound, and then suboptimal or optimal. Also the approximate starting solutions provided by the IEC algorithms are, on the average, close to optimum. The tight lower bound can also be used for testing other EC sensor location algorithms. Running times allow dealing with polygons with up to a few hundreds of edges, which appears adequate for many practical cases. An enhanced version of the algorithm, also taking into account range and incidence constraints, has also been implemented and tested.
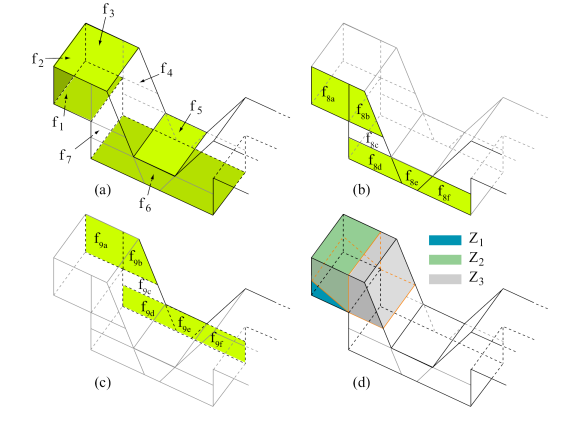
We are currently working on the extension of the previous approach to 3D, where the features to be observed in their entirety are in this case the faces of a polyhedral environment. The algorithm is, again, iterative and proceed towards the optimal solution dividing some of the faces of the object. A polyhedral specific lower bound on the number of sensors is used at each step to evalueate the quality of the current solution.
We have already developed and implemented an optimal 3D sensor location algorithms that can locate sensors into a polyhedral environment that are able to see the features of the objects in their entirety, provided the environment has certain characteristics (that is, no lines three-tangent to edges are present, since this would determine curved surfaces that are not manageable with our implementation).
A. Bottino, A. Laurentini
A Nearly Optimal Sensor Location Algorithm for Boundary Coverage
Pattern Recognition, Volume 41, Issue 11, November 2008, Pages
3343-3355 (DOI)
A. Laurentini
Guarding the Walls of an Art Gallery
The Visual Computer Journal, Vol.15, No.6 1999 (PDF)
A. Bottino
Towards an iterative algorithm for the optimal sensors
placement in a 3D environment
Internal Report #CGVG-BO01-07, October 2007
A. Bottino, A. Laurentini, L. Rosano
A Tight Lower Bound for Art Gallery Sensor Location Algorithms
Proceedings of 12th IEEE Conference on Emerging Technologies and
Factory Automation. Patras - Greece. September 25-28, 2007.
A. Bottino, A. Laurentini
Experimental Results Show Near-Optimality Of A Sensor Location
Algorithm
Proceedings of IEEE International Conference on Robotics and
Biomimetics (ROBIO 2006), Kunming, China, December 17-20, 2006
A. Bottino, A. Laurentini
Optimal positioning of sensors in 3D
Proceedings of 10th Iberoamerican Congress on Pattern Recognition
Havana, Cuba, November 15-18, 2005
A. Bottino, A. Laurentini
A practical iterative algorithm for sensor positioning
Proceedings of 10th IEEE International Conference on Emerging
Technologies and Factory Automation Catania, Italy, 19-22 September
2005
A. Bottino, A. Laurentini
A new art gallery algorithm for sensor location
Proceedings of ICINCO 2005, Barcelona (SP), September 14-17, 2005
A. Bottino, A. Laurentini
Locating sensors into a 3D polyhedral environment
Proceedings of 13th Int. Conf. on Computer Graphic, Visualization and
Computer Vision WSCG'2005, Plzen (CZ), February 1-4, 2005
Copyright © 2007 - All Rights Reserved
CG&VC
@ Politecnico
di Torino